多年前,美国一位数学家爱德华·索普,拿着粉丝资助的1万美金,来到赌城拉斯维加斯。索普先生出手不凡,屡战屡胜,不多久就引起赌场老板的“关注”。但这并没有影响事态的发展,索普先生愈战愈勇,1万美金很快翻了几番,几个赌场遭到不同程度的“血洗”。索普先生因此遭到赌场老板的封杀,以后要想过一把赌瘾,还要乔装打扮,潜入赌场。
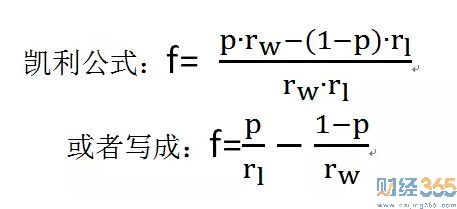
为了不影响自己的“赌兴”,索普先生把目光转移到更大的赌场——华尔街。在这里,他把用在赌场上的理论发扬光大,创立了全新的量化投资策略,并成立了第一支量化对冲基金。在上个世纪70、80年代,索普的量化对冲基金连续11年获得了超过两位数的回报。索普先生也被称为“量化投资之父”。
索普先生的投资理论博大精深,非我吃瓜群众能用一言半语解释清楚的。今天我只拿当年索普先生去赌场时用的一个小工具——凯利公式为主题,谈谈赌博和投资。
讲凯利公式之前,咱们先热热身,算几个赌博的小例子。
例1:参与概率对自己有利的游戏
假设有人要和你赌博,猜从某个学校校门里出来的是男生还是女生,猜错输掉赌注,猜对赢得对方赌注。你如果知道这个学校的男女比例是2:1,那么这就是一个概率对你有利的游戏,你的策略应该是每次都猜男生。如果初始资金是100块钱,每次都下注资金的50%,咱们现在模拟一下各种情况下最终的资金情况。

从表中可以看出,每次都下注50%的资金,参与了3次,赢了2次,最终的资金是一样,和输赢出现的顺序无关。可以推测,如果参与了300次,赢了200次,无论这200次盈利是以怎样的顺序实现,最终的结果都是一样的。
例2:参与赔率对自己有利的游戏
如果有人和你玩猜硬币的游戏,你如果猜错了,会输掉赌注;如果猜对了,除了返还赌注外,还会再额外赢得2倍赌注(1赔3)。如果猜对和猜错的概率各是50%的话,这是一个赔率对你有利的游戏,你也应该持续参与。你有100元,每次投入资金的80%,现在也模拟一下各种情况下的最终资金:
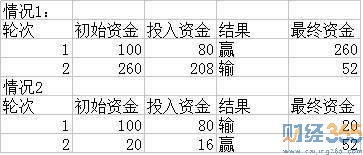
咦?怎么回事?不管是先赢再输,还是先输再赢,结果都是钱越赌越少了!再这么持续下去,来个10来轮,就剩个零头了。说好的赔率对自己有利,要持续参与呢?
其实,在赌博中能否获胜,不仅跟概率和赔率有关,还跟每次下注的比例有关。下注比例不合适,即使获胜的概率大,赔率对自己有利,也不见得能获胜。凯利公式就是专门用来解决赌博时每次下注比例的工具。
凯利公式在赌博中的应用
凯利先生等了这么久,终于该到了闪亮登场的时候了。凯利是美国贝尔实验室的物理学家,他通过研究信息论,发现赌徒可以在知道胜率和赔率的情况下,确定最优的下注比例,从而使自己的长期复合收益最大化。凯利1956年发表了一篇论文,把这个方法发表了出来。
这里需要强调一点,凯利先生虽然发明了凯利公式,但他却对赌博兴趣不大。而数学家索普看到这个论文后欣喜若狂,他把这个公式发扬光大,在赌场和华尔街赚的盆满钵满,成就了自己量化投资之父的地位。
凯利公式有几种形式,其中的一种如下:
f=p/a-q/b
其中:f表示分配的资金比例
p表示获胜的概率
q表示失败的概率
a表示失败损失率,指失败后押注的资金从1变成1-a
b表示获胜增长率,指获胜后押注的资金从1变成1+b
如果f算出来是0,表示这是一个期望收益为0的游戏,最优决策是不参加。
如果f算出来是负数,表示这是一个期望收益为负的游戏,更是不能参加了。
如果f算出来是小于1的正数,就应该按照这个比例下注;如果是个大于1的数,最优的决策是需要借钱来参与这个游戏。
对于例1来说,我们把数字代入进去:
p=2/3,q=1/3,a=1,b=1,计算出f=1/3
我们把例1重算一下,利用凯利公式,每次投入资金的1/3,结果如下表所示
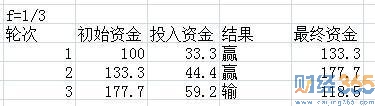
可以看出,每次下注1/3,比每次下注50%最终的收益要高。
对于例2来说,我们把数字代入进去:
p=0.5,q=0.5,a=1,b=2,计算出f=0.25
现在把例2重新计算一次,用的是凯利公式,每次押注25%的本金
可以看出,每次下注25%的资金,最终的收益不但远远高于下注80%,而且实现了正收益。看来,赌徒即使发现一个期望收益为正的游戏,如果不知道凯利公式而胡乱下注,最终也很有可能是亏损的。
大家如果感兴趣可以自己算一下,用任何其他只要不是凯利公式算出来的比例,最终的收益一定低于用凯利公式算出来的比例。
赌徒不可怕,就怕赌徒有文化啊。
凯利公式在投资中的应用
赌博和投资在很多方面都是有相通之处的。有时想一想,我们做的投资决策,如果成功的概率不是100%,何尝又不是一种赌博呢?
举例来说,某只在美国上市的中概股,原本价格是50,突然宣布要私有化退市了,私有化价格为110。消息公布后,股票价格涨到100。这时,你通过对大量的信息进行分析后,得出如下的判断:最终成功私有化退市的概率为80%,不成功的概率为20%。
那么问题来了:应该参与这次的私有化退市套利吗?如果参加,资金投入的比例应该是多少?
可以看出,如果私有化成功,获利会是10%;如果失败,亏损会是50%。这时用凯利公式代入各项数值进行计算:
p=0.8,q=0.2,a=0.5,b=0.1,算出f=-0.4
由于f是负数,所以我们不应该买入这样的股票,甚至应该做空这只股票。
但如果成功的概率是90%,失败的概率是10%的话。此时p=0.9,q=0.1,a=0.5,b=0.1,算出f=0.8
这时应该投入80%的资金参与私有化套利。(并不是全部资金的80%,而是计划参与私有化套利资金的80%)
看到这里,凯利公式就基本介绍完了。大家看完后千万不要太激动,认为自己学会了凯利公式就可以在投资中所向披靡了。投资的世界实在是太复杂,远不是一个凯利公式就能解决所有问题的。但是,通过凯利公式,我们还是能够得到一定的启发,那就是:
1. 只参与期望收益为正的游戏,期望收益为零或者为负的游戏坚决不碰;
2. 利用数学工具用量化的手段来帮助我们做投资,与凭感觉做投资相比,更具有优势;
凯利公式能否应用于交易中?
不过,要是这么简单的话,为什么股市汇市期市里有90%的人都在亏钱呢?问题在于,赌场中的每一局都是独立事件,其概率没有连续性,而金融市场却与纯赌博的系统有很大区别。市场的后一日的涨跌是有可能与前一日的涨跌相关,这也是趋势交易者的立点所在。换句话说,股票和期货市场的每次下注的结果是有连续性的,而不是纯随机的独立事件。实际市场是具有肥尾效应的,即从长期来看,小概率事件必然发生,而且在现实生活中,小概率事件发生的实际概率要远远的大于它的理论概率。从结果来看也就是更容易产生连续的亏损,一旦碰到这种肥尾,投资者将会承受极大的损失。
其次,赌场里的胜率和盈亏比都是基本固定的,因此每一次的p和b都接近真值。但是金融市场又是另一番说法。虽然我们可以通过历史数据回测计算平均胜率和盈亏比,但是这些数值只是一个统计量,我们所获得的也都是平均值。实际亏损很可能会超过平均值,这就导致了使用p和b的平均数去计算凯利公式的f值会偏大。譬如,你碰到了连续3次1.5倍平均值的亏损,那么你将会发生一次十分巨大的回撤,而凯利公式中的均值将这些偏大的亏损都给平均了。
因此,需要明确的是,凯利公式的首要目的不是提高资产增长率,而是控制极端风险。在解决实际应用问题上,凯利公式所针对的投注比例并不是相较于全资产而言,而是投资者可以承受损失的资产。也就是说,在运用凯利公式解决实际应用问题时,投资者可以根据自身交易系统所计算出的f值乘以心理承受损失比例去控制最大仓位。
反过来看,凯利公式也能用来检验交易系统能否被心理所承受。假设盈亏比设定为2:1,每次采用40%的投注比例,那么需要胜率达60%最适合。如果投资者的原有系统低于这个胜率,这就证明系统需要优化,否则将不得不承受连续亏损造成账户大幅回撤带来的心理压力。
 本文来源:
本文来源: